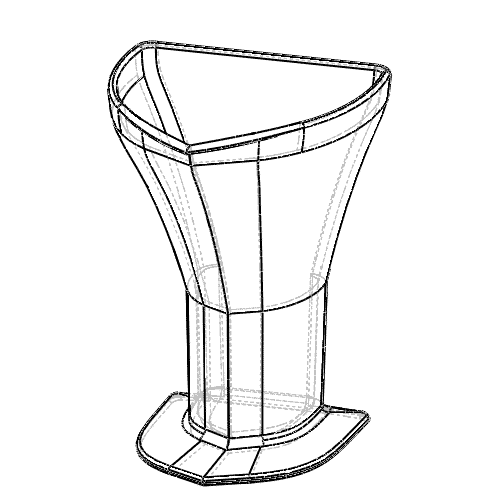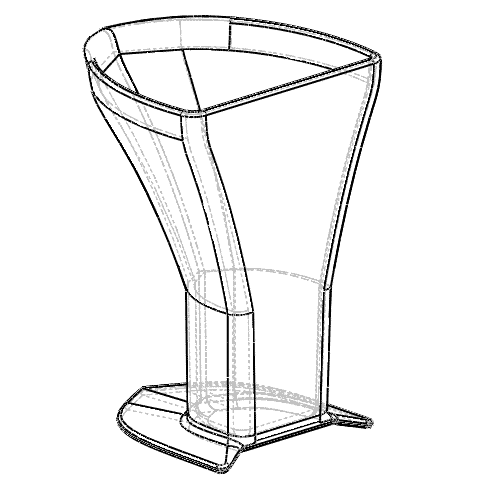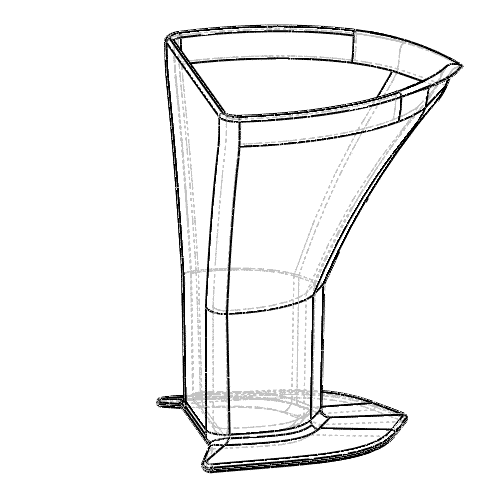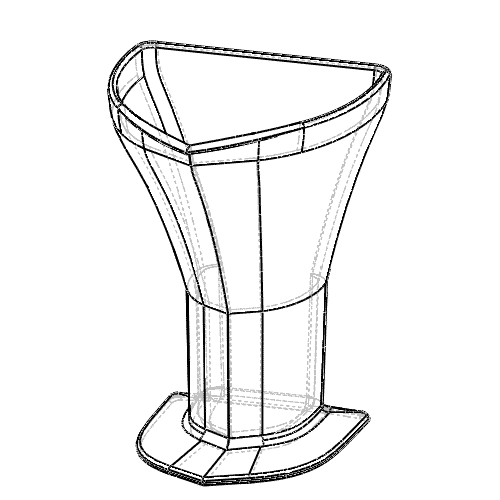
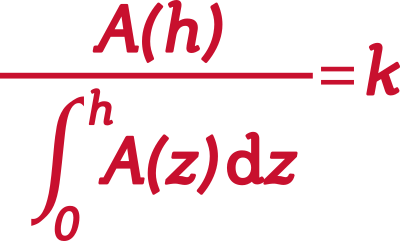This page requires javascript to be enabled.

There’s math behind accurate measuring.

Accurate measuring starts with an accurate measuring cup. In a magical world where the lines are all in the right place and you could pour exactly to the line, perfect measuring would be a given.
Rotating Euclid
Example of error due to liquid sloshing in measuring cup

But in the real world, shape matters too.

It can be tricky to tell exactly how close you are to the line, even if you're being careful. This could be because liquid is sloshing around in the cup, or you're not holding the cup at exactly eye level and so forth. In fact, it's even difficult to get it exactly right in a laboratory setting.
Example of error due to liquid sloshing in measuring cup


If the contents end up a little above or below the line, the shape of the measuring cup dramatically affects the resulting error. Which makes the next question: What is the optimal shape? (Hint, it's Euclid.)

The link is the ratio of surface area to volume.

To illustrate, let's get concrete and look at the error if you're trying to measure 1 cup, and you overshoot the line by 1mm. In this case, you have 1 cup of liquid plus a thin layer of extra liquid that's 1mm thick.

The volume of that extra liquid equals 1mm times the surface area of the extra layer. The error equals the extra volume divided by the target volume (1 cup) times 100, to make it a percent. This is how it looks:
Showing 1mm slice of extra liquid and equations
In other words, the error if you overshoot the line depends on the ratio of surface area to volume at that line. This is true whether you're careful and get to within 1mm of the line, or you’re in pour-and-go mode and miss by 20mm.

Traditional cups are inconsistent.

In all existing measuring cups before Euclid (whether they're traditional or conically shaped), that ratio of surface area to volume increases for lines lower down in the cup. This means that the cup measures less accurately at lower lines. If the cup is shaped like a cylinder, it's 4x worse measuring 1/4 cup than 1 cup. Conically shaped cups help somewhat, but still result in the same problem.

In contrast, Euclid tapers to keep the ratio constant, so it measures small amounts just as accurately as large amounts.
Surface area
Volume
Traditional Measuring Cup
Surface area
Volume
Euclid logo

So why Euclid's equation?

The equation printed on Euclid mathematical expresses its secret: a shape that maintains the same ratio of surface area to volume at every measurement line.

A(h) represents the surface area at a height, h. The integral captures the volume at that height h.
Surface Area
Volume
Euclid equation
Constant Proportion
Euclid is named after Euclid of Alexandria, who is considered the founding father of geometry.
Questions
Email us at info@euclidmeasuring.com
Media
Visit our Media folder
X
Web page is out of date due to server upgrade.
Please reload page.